Power flow study

In power engineering, the power flow study (also known as load-flow study) is an important tool involving numerical analysis applied to a power system. A power flow study usually uses simplified notation such as a one-line diagram and per-unit system, and focuses on various forms of AC power (ie: voltages, voltage angles, real power and reactive power). It analyzes the power systems in normal steady-state operation. There exists a number of software implementations of power flow studies.

In addition to a power flow study, sometimes called the base case, many software implementations perform other types of analysis, such as short-circuit fault analysis, stability studies (transient & steady-state), unit commitment and economic load dispatch analysis. In particular, some programs use linear programming to find the optimal power flow, the conditions which give the lowest cost per kilowatthour delivered.

Power flow or load-flow studies are important for planning future expansion of power systems as well as in determining the best operation of existing systems. The principal information obtained from the power flow study is the magnitude and phase angle of the voltage at each bus, and the real and reactive power flowing in each line.

Commercial power systems are usually too large to allow for hand solution of the power flow. Special purpose network analyzers were built between 1929 and the early 1960s to provide laboratory models of power systems; large-scale digital computers replaced the analog methods.

1 Power flow problem formulation
2 Newton-Raphson solution method
3 Power flow methods
4 References

Power flow problem formulation

The goal of a power flow study is to obtain complete voltage angle and magnitude information for each bus in a power system for specified load and generator real power and voltage conditions.^[1] Once this information is known, real and reactive power flow on each branch as well as generator reactive power output can be analytically determined. Due to the nonlinear nature of this problem, numerical methods are employed to obtain a solution that is within an acceptable tolerance.

The solution to the power flow problem begins with identifying the known and unknown variables in the system. The known and unknown variables are dependent on the type of bus. A bus without any generators connected to it is called a Load Bus. With one exception, a bus with at least one generator connected to it is called a Generator Bus. The exception is one arbitrarily-selected bus that has a generator. This bus is referred to as the Slack Bus.

In the power flow problem, it is assumed that the real power P_D and reactive power Q_D at each Load Bus are known. For this reason, Load Buses are also known as PQ Buses. For Generator Buses, it is assumed that the real power generated P_G and the voltage magnitude |V| is known. For the Slack Bus, it is assumed that the voltage magnitude |V| and voltage phase Θ are known. Therefore, for each Load Bus, both the voltage magnitude and angle are unknown and must be solved for; for each Generator Bus, the voltage angle must be solved for; there are no variables that must be solved for the Slack Bus. In a system with N buses and R generators, there are then 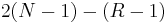$2(N-1) - (R-1)$ unknowns.

In order to solve for the 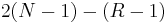$2(N-1) - (R-1)$ unknowns, there must be 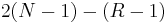$2(N-1) - (R-1)$ equations that do not introduce any new unknown variables. The possible equations to use are power balance equations, which can be written for real and reactive power for each bus. The real power balance equation is:

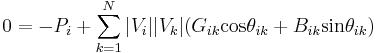
$0 = -P_{i} %2B \sum_{k=1}^{N}|V_{i}||V_{k}|(G_{ik}\mbox{cos}\theta_{ik}%2BB_{ik}\mbox{sin}\theta_{ik})$

where 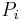$P_{i}$ is the net power injected at bus i, 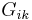$G_{ik}$ is the real part of the element in the bus admittance matrix Y_BUS corresponding to the ith row and kth column, 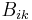$B_{ik}$ is the imaginary part of the element in the Y_BUS corresponding to the ith row and kth column and 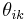$\theta_{ik}$ is the difference in voltage angle between the ith and kth buses. The reactive power balance equation is:

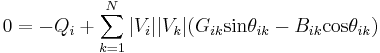
$0 = -Q_{i} %2B \sum_{k=1}^{N}|V_{i}||V_{k}|(G_{ik}\mbox{sin}\theta_{ik}-B_{ik}\mbox{cos}\theta_{ik})$

where 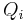$Q_{i}$ is the net reactive power injected at bus i.

Equations included are the real and reactive power balance equations for each Load Bus and the real power balance equation for each Generator Bus. Only the real power balance equation is written for a Generator Bus because the net reactive power injected is not assumed to be known and therefore including the reactive power balance equation would result in an additional unknown variable. For similar reasons, there are no equations written for the Slack Bus.

Newton-Raphson solution method

There are several different methods of solving the resulting nonlinear system of equations. The most popular is known as the Newton-Raphson Method. This method begins with initial guesses of all unknown variables (voltage magnitude and angles at Load Buses and voltage angles at Generator Buses). Next, a Taylor Series is written, with the higher order terms ignored, for each of the power balance equations included in the system of equations . The result is a linear system of equations that can be expressed as:

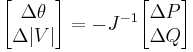
$\begin{bmatrix}\Delta \theta \\ \Delta |V|\end{bmatrix} = -J^{-1} \begin{bmatrix}\Delta P \\ \Delta Q \end{bmatrix}$

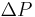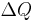where $\Delta P$ and $\Delta Q$ are called the mismatch equations:

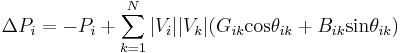
$\Delta P_{i} = -P_{i} %2B \sum_{k=1}^{N}|V_{i}||V_{k}|(G_{ik}\mbox{cos}\theta_{ik}%2BB_{ik}\mbox{sin}\theta_{ik})$

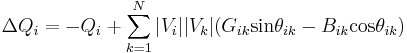
$\Delta Q_{i} = -Q_{i} %2B \sum_{k=1}^{N}|V_{i}||V_{k}|(G_{ik}\mbox{sin}\theta_{ik}-B_{ik}\mbox{cos}\theta_{ik})$

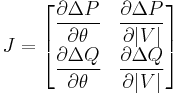and $J$ is a matrix of partial derivatives known as a Jacobian: $J=\begin{bmatrix} \dfrac{\partial \Delta P}{\partial\theta} & \dfrac{\partial \Delta P}{\partial |V|} \\ \dfrac{\partial \Delta Q}{\partial \theta}& \dfrac{\partial \Delta Q}{\partial |V|}\end{bmatrix}$ .

The linearized system of equations is solved to determine the next guess (m + 1) of voltage magnitude and angles based on:

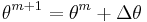
$\theta^{m%2B1} = \theta^{m} %2B \Delta \theta\,$

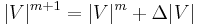
$|V|^{m%2B1} = |V|^{m} %2B \Delta |V|\,$

The process continues until a stopping condition is met. A common stopping condition is to terminate if the norm of the mismatch equations is below a specified tolerance.

A rough outline of solution of the power flow problem is:

Make an initial guess of all unknown voltage magnitudes and angles. It is common to use a "flat start" in which all voltage angles are set to zero and all voltage magnitudes are set to 1.0 p.u.
Solve the power balance equations using the most recent voltage angle and magnitude values.
Linearize the system around the most recent voltage angle and magnitude values
Solve for the change in voltage angle and magnitude
Update the voltage magnitude and angles
Check the stopping conditions, if met then terminate, else go to step 2.

Power flow methods

Newton–Raphson method
Fast-Decoupled-Load-Flow method
Gauss Iterative method
Gauss–Seidel method

References

^ J. Grainger and W. Stevenson, Power System Analysis, McGraw-Hill, New York, 1994, ISBN 0-07-061293-5

Power flow study

Contents

Power flow problem formulation

Newton-Raphson solution method

Power flow methods

References